MOLCAS manual:

Next: 6.15 Other Multiconfigurational and Multireference
Up: 6. Program Based Tutorials
Previous: 6.13 CPF A
Subsections
6.14 CCSDT — A Set of Coupled-Cluster Programs
The MOLCAS program CCSDT
computes Coupled-Cluster Singles Doubles, CCSD, and Coupled-Cluster Singles
Doubles and Non-iterative Triples Correction CCSD(T) wave functions
for restricted single reference
both closed- and open-shell systems.
In addition to the ONEINT and ORDINT integral files
(in non-Cholesky calculations),
the CCSDT code requires the JOBIPH file containing the
reference wave function (remember that it is not possible to
compute open-shell systems with the SCF program) and
the transformed two-electron integrals produced by the MOTRA
module and stored in the TRAINT file.
Previously to execute the CCSDT module, wave functions
and integrals have to be prepared. First, a RASSCF calculation has
to be run in such a way that the resulting wave function has one
single reference. In closed-shell situations this means to include
all the orbitals as inactive and set the number of active electrons to zero.
Keyword OUTOrbitals followed by the specification CANOnical
must be used in
the RASSCF input to activate the construction of canonical
orbitals and the calculation of the CI-vectors on the basis of
the canonical orbitals.
After that the MOTRA module has to
be run to transform the two-electron integrals using the molecular
orbitals provided by the RASSCF module.
The files JOBIPH or RASORB from the
RASSCF calculation can be used directly by MOTRA
using the keywords JOBIph or LUMOrb in the MOTRA input.
Frozen or
deleted orbitals can be introduced in the transformation step
by the proper options in the MOTRA input.
The section of the MOLCAS output corresponding to the CC program
is self explanatory. The default output simply contains
the wave function specifications from the previous RASSCF calculation,
the orbital specifications, the diagonal Fock matrix elements and orbital
energies, the technical description of the calculation, the iterations leading to the CCSD energy,
and the five largest amplitudes of each type, which will help to evaluate
the calculation. If triples excitations have been required the description
of the employed method (from the three available) to compute perturbatively
the triple excited contributions to the CC energy, the value of the
correction, and the energy decomposition into spin parts will be available.
Figure 6.13 contains the input files required by the
seward, scf,
rasscf, motra and ccsdt
programs to compute the ground state of the HF+ cation.
molecule, which is a doublet of 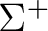 symmetry. A more detailed
description of the different options included in the input of the
programs can be found in the CCSDT section of the user's guide.
This example describes how to calculate CCSD(T) energy for HF(+) cation.
This cation can be safely represented by the single determinant as a reference
function, so one can assume that CCSD(T) method will be suitable for its
description. symmetry. A more detailed
description of the different options included in the input of the
programs can be found in the CCSDT section of the user's guide.
This example describes how to calculate CCSD(T) energy for HF(+) cation.
This cation can be safely represented by the single determinant as a reference
function, so one can assume that CCSD(T) method will be suitable for its
description.
The calculation can be divided into few steps:
- Run SEWARD to generate AO integrals.
- Calculate the HF molecule at the one electron level using SCF to
prepare an estimate of MO for the RASSCF run.
- Calculate HF(+) cation by subtracting one electron from the orbital with
the first symmetry. There is only one electron in one active orbital
so only one configuration is created. Hence, we obtain a simple single
determinant ROHF reference.
- Perform MO transformation exploiting MOTRA using MO coefficients
from the RASSCF run.
- Perform the Coupled Cluster calculation using CCSDT program. First,
the data produced by the programs RASSCF and MOTRA need
to be reorganized, then the CCSD calculation follows, with the chosen spin
adaptation being T2 DDVV. Finally, the noniterative triple excitation contribution
calculation is following, where the CCSD amplitudes are used.
This is an open shell case, so it is suitable to choose CCSD(T) method
as it is defined by Watts et al. [16].
Since CCSD amplitudes produced by previous CCSD run are partly
spin adapted and denominators are produced from the corresponding diagonal
Fock matrix elements,
final energy is sometimes referred as SA1
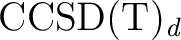 (see
[17]). (see
[17]).
Figure 6.13:
Sample input containing the files required by the SEWARD, SCF,RASSCF, MOTRA, CCSORT, CCSD, andCCT3 programs to compute the ground state of the HF+ cation.
 |
&SEWARD &END
Title= HF molecule
Symmetry
X Y
Basis set
F.ANO-S-VDZ
F 0.00000 0.00000 1.73300
End of basis
Basis set
H.ANO-S-VDZ
H 0.00000 0.00000 0.00000
End of basis
End of input
&SCF
&RASSCF
Title= HF(+) cation
OUTOrbitals= Canonical
Symmetry= 1; Spin= 2
nActEl= 1 0 0; Inactive= 2 1 1 0; Ras2= 1 0 0 0
LumOrb; OUTOrbitals= Canonical
&MOTRA; JobIph; Frozen= 1 0 0 0
&CCSDT
Iterations= 50; Shift= 0.2,0.2; Accuracy= 1.0d-7
Denominators= 2; Extrapolation= 5,4
Adaptation= 1; Triples= 3; T3Denominators= 0
RASSCF calculates the HF ionized state by removing one electron
from the orbital in the first symmetry.
Do not forget to use keyword
CANONICAL.
In the CCSDT run, the number of iterations is limited to 50.
Denominators will be formed using orbital energies. (This corresponds to the
chosen spin adaptation.) Orbitals will be shifted by 0.2 au,
what will accelerate the convergence. However, final energy will not be
affected by the chosen type of denominators and orbital shifts. Required
accuracy is 1.0d-7 au. for the energy. T2 DDVV class of CCSD amplitudes will
be spin adapted.
To accelerate the convergence,
DIIS procedure is exploited. It will start after 5th iteration and
the last four iterations will be taken into account in each extrapolation step.
In the triples step the CCSD(T) procedure as defined
by Watts et al. [16] will be performed.
Corresponding denominators will be produced using diagonal Fock matrix elements.
| Keyword | Meaning
|
| CCSD | Coupled-cluster singles and doubles method
|
| CCT | CCSD plus a non iterative triples (T) calculation
|
|
|
Next: 6.15 Other Multiconfigurational and Multireference
Up: 6. Program Based Tutorials
Previous: 6.13 CPF A
|


























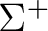 symmetry. A more detailed
description of the different options included in the input of the
programs can be found in the CCSDT section of the user's guide.
This example describes how to calculate CCSD(T) energy for HF(+) cation.
This cation can be safely represented by the single determinant as a reference
function, so one can assume that CCSD(T) method will be suitable for its
description.
symmetry. A more detailed
description of the different options included in the input of the
programs can be found in the CCSDT section of the user's guide.
This example describes how to calculate CCSD(T) energy for HF(+) cation.
This cation can be safely represented by the single determinant as a reference
function, so one can assume that CCSD(T) method will be suitable for its
description.
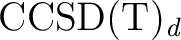 (see
[
(see
[