





















MOLCAS manual: Next: 8.47 SlapAf Up: 8. Programs Previous: 8.45 seward 8.46 single_anisoThe SINGLE_ANISO program is a routine which allows the non-perturbative calculation of effective spin (pseudospin) Hamiltonians and static magnetic properties of mononuclear complexes and fragments completely ab initio, including the spin-orbit interaction. As a starting point it uses the results of RASSI calculation for the ground and several excited spin-orbital multiplets. A short description of methodology and applications can be found in [150], [151]. The second version of the SINGLE_ANISO program is able to calculate the following quantities:
The magnetic Hamiltonians are defined for a desired group of N electronic states obtained in RASSI calculation to which a pseudospin S̃ (it reduces to a true spin S in the absence of spin-orbit coupling) is subscribed according to the relation N=2S̃+1. For instance, the two wave functions of a Kramers doublet correspond to S̃=1/2. The implementation is done for S̃=1/2, 1, 3/2, ... ,15/2. The calculation of magnetic properties takes into account the contribution of excited states (the ligand-field and charge transfer states of the complex or mononuclear fragment included in the RASSI calculation) via their thermal population and Zeeman admixture. The intermolecular exchange interaction between magnetic molecules in a crystal can be taken into account during the simulation of magnetic properties by a phenomenological parameter zJ specified by the user (see keyword MLTP).
The SINGLE_ANISO program takes all needed ab initio information from the RUNFILE: i.e. matrix elements of angular momentum, spin-orbit energy spectrum and mixing coefficients, number of mixed states and their multiplicity, etc. In order to find the necessary information in the RUNFILE, the keywords MEES and SPIN are mandatory for RASSI. The SEWARD keyword ANGM is also compulsory.
|
| File | Contents |
| RUNFILE | The file of communication between different modules in MOLCAS. Its presence is mandatory when the calculation is not a restart one from a data file. |
8.46.2.2 Restart files & options
| File | Contents |
| RUNFILE | The file of communication between different modules in MOLCAS. Normally it is already present in $WorkDir. The SINGLE_ANISO may be restarted as many times as necessary in the same working directory where the previous RASSI was succesfully executed. The RUNFILE contains then all necessary data. |
| ANISOINPUT | The program may be restarted from the ASCII text file ANISOINPUT generated by a previous succesful run of the SINGLE_ANISO (the name of this file may be specified during execution, see REST keyword below). This file contains all necessary data for SINGLE_ANISO as well as for the POLY_ANISO. In this case the initial $WorkDir may be empty (RUNFILE is not necessary). |
| $Project.aniso | The SINGLE_ANISO may be restarted from the binary file $Project.aniso produced in a previous run. The initial $WorkDir may be empty (RUNFILE is not necessary). |
8.46.2.3 Output files
| File | Contents |
| $Project.aniso | This binary file may be used for restart. It is produced by any successful run of the code. |
| ANISOINPUT | This file is intended to be as input for the POLY_ANISO module in MOLCAS. It is an ASCII formated file. It is produced by any successful run of the code. |
| zeeman_energy_xxx.txt | Zeeman eignestates for the applied field in the direction # xxx are placed in the corresponding text file. It may be used directly with external plotting programs like gnuplot to visualize the data. |
| XT_compare.txt | In case TEXP is employed (experimental XT(T) data points), the SINGLE_ANISO produces a data file used to directly plot the comparison between experimental and calculated magnetic susceptibility. |
| MH_compare_xxx.txt | In case HEXP is employed (experimental M(H,T) data points), the SINGLE_ANISO produces one or several data file(s) used to directly plot the comparison(s) between experimental and calculated molar magnetization at each temperature. |
8.46.3 Input
Normally SINGLE_ANISO runs without specifying any of the following keywords. The only unknown variable for SINGLE_ANISO is the dimension (multiplicity) of the pseudospin. By default one multiplet is selected, which has the dimension equal to the multiplicity of the ground term. For example, in cases where spin-orbit coupling is weak, the multiplicity of the effective spin Hamiltonian is usually the same as the multiplicity of the lowest term, while in the cases with strong anisotropy (lanthanide or actinide complexes, Co2+ complexes, etc...) the lowest energy levels of the complexes form a group of states which can differ quite strong from the spin multiplicity of the lowest term. In these cases the user should specify the multiplicity corresponding to a chosen value of pseudospin (2S̃+1). For instance, in Dy3+ the spin of the ground state term is S=5/2, but in many situations only the ground Kramers doublet is considered; then the user should set the multiplicity of the pseudospin equal to 2 (see MLTP keyword). The calculation of the parameters of the crystal field corresponding to the ground atomic multiplet for lanthanides should be requested by the CRYS keyword.
&SINGLE_ANISO
Argument(s) to a keyword are always supplied on the next line of the input file.
8.46.3.1 Optional general keywords to control the input
| Keyword | Meaning | |
| TITLe | One line following this one is regarded as title.
| |
| TYPE | This keyword is obsolete.
| |
| MLTP | The number of molecular multiplets (i.e. groups of spin-orbital eigenstates) for which g, D and higher magnetic tensors will be calculated (default MLTP=1). The program reads two lines: the first is the number of multiplets (nmult) and the second the array of nmult numbers specifying the dimension of each multiplet. By default, the code will first analyze the energy spectra by itself and will compute the g and D tensors for ten low-lying groups of states. By using this keyword the user overwrites the default.
Example:
| |
| TINT | Specifies the temperature points for the evaluation of the magnetic susceptibility. The program will read four numbers: Tmin, Tmax, nT.
TINT 0.0 330.0 331 SINGLE_ANISO will compute temperature dependence of the magnetic susceptibility in 331 points evenly distributed in temperature interval: 0.0K – 330.0K.
| |
| HINT | Specifies the field points for the evaluation of the magnetization in a certain direction. The program will read four numbers: Hmin, Hmax, nH.
HINT 0.0 20.0 201 SINGLE_ANISO will compute the molar magnetization in 201 points evenly distributed in field interval: 0.0T – 20.0T.
| |
| TMAG | Specifies the temperature(s) at which the field-dependent magnetization is calculated. The program will read the number of temperature points (NTemp) and then an array of real numbers specifying the temperatures (in Kelvin) at which magnetization is to be computed.
Default is to compute magnetization at one temperature point (2.0 K).
Example:
TMAG 5 1.8 2.0 3.4 4.0 5.0 SINGLE_ANISO will compute the molar magnetization at 5 temperature points (1.8 K, 2.0 K, 3.4 K, 4.0 K, and 5.0 K).
| |
| ENCU | This flag is used to define the cut-off energy for the lowest states for which
Zeeman interaction is taken into account exactly. The contribution to the magnetization
arising from states that are higher in energy than E (see below) is done by
second-order perturbation theory. The program will read two integer
numbers: NK and MG. Default values are: NK=100,MG=100.
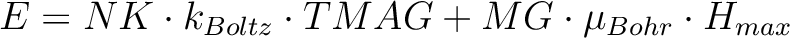
The field-dependent magnetization is calculated at the temperature value TMAG. Example: ENCU 250 150 If Hmax = 10T and TMAG=1.8K, then the cut-off energy is: 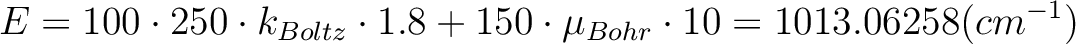
This means that the magnetization coming from all spin-orbit states with energy lower than E=1013.06258 (cm-1) will be computed exactly. The contribution from the spin-orbit states with higher energy is accounted by second-order perturbation.
| |
| NCUT | This flag is used to define the cut-off energy for the lowest states for which
Zeeman interaction is taken into account exactly. The contribution to the magnetization
arising from states that are higher in energy than lowest NCUT states, is done by
second-order perturbation theory. The program will read one integer number. In case the number
is larger than the total number of spin-orbit states(NSS, then the NCUT is set to NSS
(which means that the molar magnetization will be computed exactly, using full Zeeman
diagonalization for all field points). The field-dependent magnetization is calculated at
the temperature value(s) defined by TMAG.
Example:
NCUT 32
| |
| MVEC | Defines the number of directions for which the magnetization vector will be computed.
On the first line below the keyword, the number of directions should be mentioned (NDIR. Default 0).
The program will read NDIR lines for cartesian coordinates specifying the direction i of the
applied magnetic field (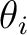 and and 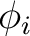 ). These values may be arbitrary real numbers.
The direction(s) of applied magnetic field are obtained by normalizing the length of each vector to one.
Example: ). These values may be arbitrary real numbers.
The direction(s) of applied magnetic field are obtained by normalizing the length of each vector to one.
Example:
MVEC 4 0.0000 0.0000 0.1000 1.5707 0.0000 2.5000 1.5707 1.5707 1.0000 0.4257 0.4187 0.0000 The above input requests computation of the magnetization vector in four directions of applied field. The actual directions on the unit sphere are: 4 0.00000 0.00000 1.00000 0.53199 0.00000 0.84675 0.53199 0.53199 0.33870 0.17475 0.17188 0.00000
| |
| MAVE | This keyword specifies the grid density used for the computation of powder molar
magnetization. The program uses Lebedev-Laikov distribution of points on the unit sphere.
The program reads two integer numbers: nsym and ngrid. The nsym defines which
part of the sphere is used for averaging. It takes one of the three values: 1 (half-sphere),
2 (a quater of a sphere) or 3 (an octant of the sphere). ngrid takes values from 1
(the smallest grid) till 32 (the largest grid, i.e. the densiest). The default is to
consider integration over a half-sphere (since M(H)=-M(-H)): nsym=1 and ngrid=15
(i.e 185 points distributed over half-sphere). In case of symmetric compounds, powder
magnetization may be averaged over a smaller part of the sphere, reducing thus the number
of points for the integration. The user is responsible to choose the appropriate integration scheme.
Note that the programś default is rather conservative.
| |
| TEXP | This keyword allows computation of the magnetic susceptibility 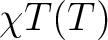 at experimental points.
On the line below the keyword, the number of experimental points NT is defined, and on
the next NT lines the program reads the experimental temperature (in Kelvin) and the
experimental magnetic susceptibility (in cm3Kmol-1 ).
TEXP and TINT keywords are mutually exclusive. The magnetic susceptibility
routine will also print the total average standard deviation from the experiment. at experimental points.
On the line below the keyword, the number of experimental points NT is defined, and on
the next NT lines the program reads the experimental temperature (in Kelvin) and the
experimental magnetic susceptibility (in cm3Kmol-1 ).
TEXP and TINT keywords are mutually exclusive. The magnetic susceptibility
routine will also print the total average standard deviation from the experiment.
| |
| HEXP | This keyword allows computation of the molar magnetization Mmol (H) at experimental points.
On the line below the keyword, the number of experimental points NH is defined, and on the next NH lines
the program reads the experimental field strength (in Tesla) and the experimental magnetization (in 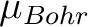 ).
HEXP and HINT are mutually exclusive. The magnetization routine will print the standard deviation from the experiment. ).
HEXP and HINT are mutually exclusive. The magnetization routine will print the standard deviation from the experiment.
| |
| ZJPR | This keyword specifies the value (in cm-1) of a phenomenological parameter of a mean
molecular field acting on the spin of the complex (the average intermolecular exchange
constant). It is used in the calculation of all magnetic properties (not for pseudo-spin
Hamiltonians) (Default is 0.0)
| |
| PRLV | This keyword controls the print level.
| |
| POLY | The keyword is obsolete. The SINGLE_ANISO creates by default one ASCII formated text file named ANISOINPUT
and also a binary file named $Project.Aniso. Both may be used to restart (or re-run again) the SINGLE_ANISO calculation.
| |
| CRYS | This keyword will enables the computation of the parameters of the crystal-field acting on the ground atomic multiplet of a
lanthanide from the ab initio calculation performed. The implemented methodology is described [153] and [152].
Two types of crystal field parametererization are implemented:
| |
| QUAX | This keyword controls the quantization axis for the computation of the Crystal-Field parameters acting on the ground atomic multiplet of a lanthanide. On the next line, the program will read one of the three values: 1, 2 or 3.
| |
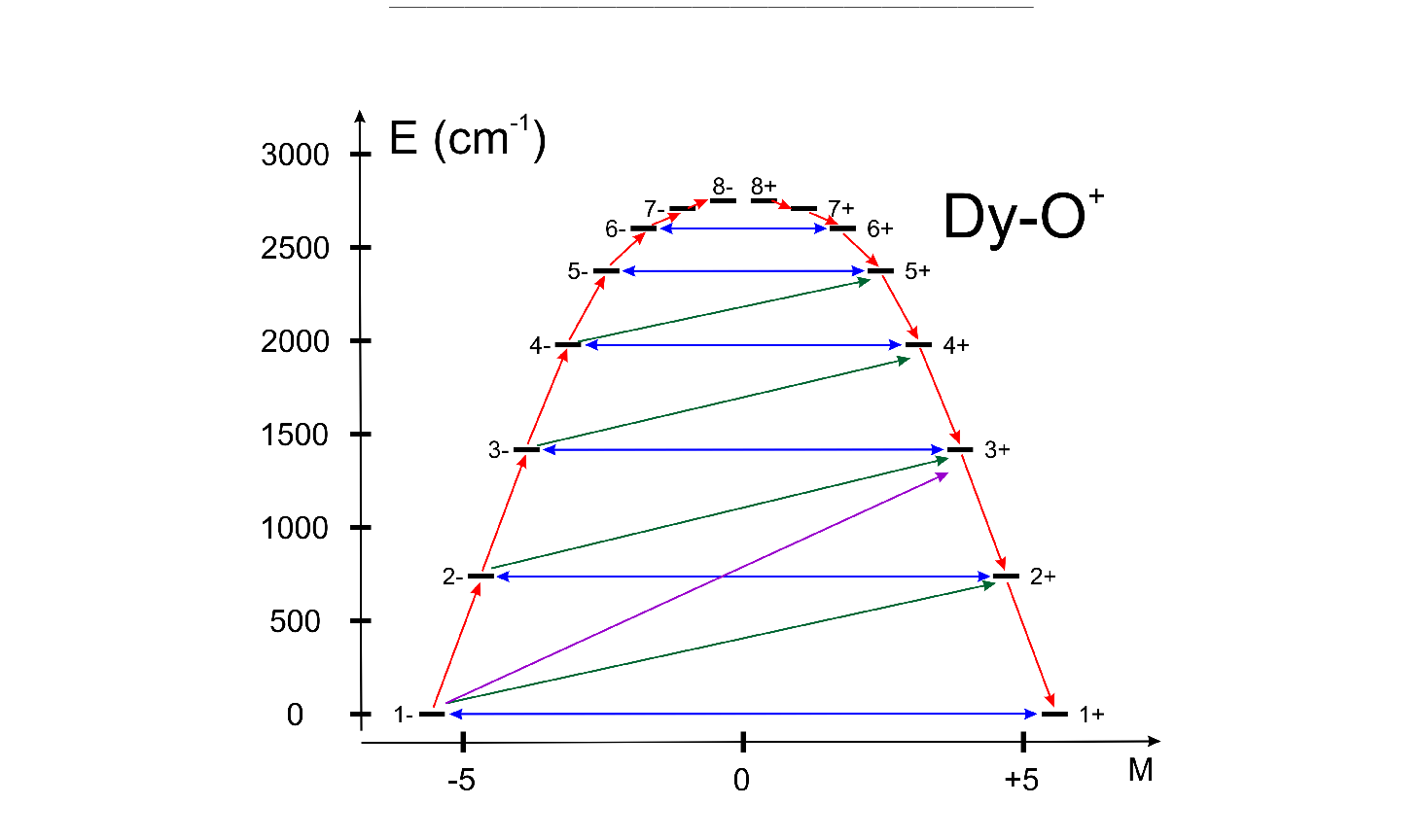
| UBAR | This keyword allows estimation of the structuere of the blocking barier of a single-molecule magnet. The default is not to compute it.
The method prints transition matix elements of the magnetic moment according to the Figure ![[*]](crossref.png) . .
All transition matrix elements of the magnetic moment are given as
(
| |
| ABCC | This keyword will enable computation of magnetic and anisotropy axes in the
crystallographic abc system. On the next line, the program will read six real
values, namely a, b, c, 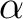 , , 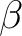 , and , and 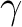 , defining the
crystal lattice. On the second line, the program will read the Cartesian coordinates
of the magnetic center. The computed values in the output correspond to the
crystallographic position of three "dummy atoms" located on the corresponding anisotropy axes, at the distance of 1 Ångstrom from the metal site. , defining the
crystal lattice. On the second line, the program will read the Cartesian coordinates
of the magnetic center. The computed values in the output correspond to the
crystallographic position of three "dummy atoms" located on the corresponding anisotropy axes, at the distance of 1 Ångstrom from the metal site.
|
8.46.3.2 An input example
&SINGLE_ANISO
MLTP
3
4 4 2
ZJPR
-0.2
ENCU
250 400
HINT
0.0 20.0 101
TINT
0.0 330.0 331
MAVE
1 12
MVEC
3
0.0000 0.0000 0.1000
1.5707 0.0000 0.5000
1.5707 1.5707 1.0000
Next: 8.47 SlapAf Up: 8. Programs Previous: 8.45 seward


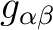 , its main values, including the sign of the product
, its main values, including the sign of the product
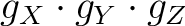 , and the main magnetic axes.
, and the main magnetic axes.
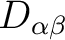 , its main values and the anisotropy axes. The anisotropy axes are given in two coordinate systems: a) in the initial Cartesian coordinate system (x, y, z) and b) in the coordinate system of the main magnetic axes (Xm, Ym, Zm).
, its main values and the anisotropy axes. The anisotropy axes are given in two coordinate systems: a) in the initial Cartesian coordinate system (x, y, z) and b) in the coordinate system of the main magnetic axes (Xm, Ym, Zm).
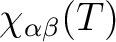
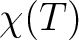
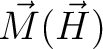 for specified directions of the applied magnetic field
for specified directions of the applied magnetic field 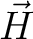
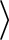 each, while
the other two groups of states being Kramers doublets.
each, while
the other two groups of states being Kramers doublets.
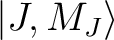 group of spin-orbit states (e.g. parameterisation of the ground J=15/2 of a Dy3+ complex).
group of spin-orbit states (e.g. parameterisation of the ground J=15/2 of a Dy3+ complex).
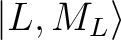 group of spin-free states (e.g. parameterisation of the ground 6H multiplet of a Dy3+).
group of spin-free states (e.g. parameterisation of the ground 6H multiplet of a Dy3+).
 .
.
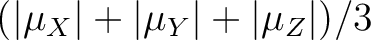 ).
The data is given in Bohr magnetons (
).
The data is given in Bohr magnetons (