





















MOLCAS manual: Next: 8.19 geo Up: 8. Programs Previous: 8.17 gateway
GENANO is a program for
determining the contraction coefficients for
generally contracted basis sets [52].
They are determined by diagonalizing a density matrix,
using the eigenvectors (natural orbitals) as
the contraction coefficients, resulting
in basis sets of the ANO (Atomic Natural Orbitals)
type [53].
|
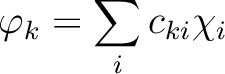 |
(8.5) |
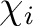 is the i'th primitive basis function.
is the i'th primitive basis function.
As a generalization to this approach we can
average over density
matrices from several wave functions, resulting
in basis sets of the density matrix averaged ANO type,
see for example [54,55,56,57].
We can view the averaging of density matrices as a sequence
of rank-1 updates in the same way as in equation ![[*]](crossref.png) .
We have more update vectors than the rank of the matrix, but this
does not really change anything. The important observation is
that all
.
We have more update vectors than the rank of the matrix, but this
does not really change anything. The important observation is
that all  's are positive and no information is lost
in the averaging.
's are positive and no information is lost
in the averaging.
The general guideline for which wave functions to include is based on what you want to be able to describe. All wave functions you want an accurate description of should be included in the averaging.
As an example, let us consider the oxygen atom.
We want to be able to describe the atom by itself accurately,
thus a wave function for the atom is needed, usually at the CI level.
In molecular systems, oxygen usually has a negative charge, thus
including  is almost mandatory.
A basis set derived from these two wave function is well
balanced for the majority of systems containing oxygen.
A logical conclusion would be that you need to include a few
molecular wave functions of systems containing oxygen, but in
practice this is not necessary. This is due to the fact that
the degrees of freedom describing the orbital shape distortion
when forming bonds are virtually identical to the lowest
correlating orbitals.
On the other hand, a few molecular species have oxygen with
positive charge, thus it may be appropriate to include
is almost mandatory.
A basis set derived from these two wave function is well
balanced for the majority of systems containing oxygen.
A logical conclusion would be that you need to include a few
molecular wave functions of systems containing oxygen, but in
practice this is not necessary. This is due to the fact that
the degrees of freedom describing the orbital shape distortion
when forming bonds are virtually identical to the lowest
correlating orbitals.
On the other hand, a few molecular species have oxygen with
positive charge, thus it may be appropriate to include
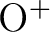 in the basis set.
in the basis set.
A wide range of specialized basis sets can also be generated,
for example a molecular basis set describing Rydberg orbitals,
see the example in the ``Tutorials and Examples'' part,
section ![[*]](crossref.png) .
There is a possibility to create rydberg orbitals
automatically by using the keyword
RYDBERG. Here all unoccupied orbitals with
negative orbital energies will be used with the associated
occupation numbers
.
There is a possibility to create rydberg orbitals
automatically by using the keyword
RYDBERG. Here all unoccupied orbitals with
negative orbital energies will be used with the associated
occupation numbers
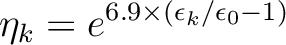 |
(8.6) |
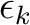 is the orbital energy of orbital k and
is the orbital energy of orbital k and
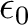 is the lowest orbital energy of all
virtual orbitals. In order to use this option you need
to use the
SCF or RASSCF program to compute
the orbitals for a cationic system.
is the lowest orbital energy of all
virtual orbitals. In order to use this option you need
to use the
SCF or RASSCF program to compute
the orbitals for a cationic system.
You need one or more wave functions, represented by formatted orbital files, to generate the average density matrix. These natural orbital files can be produced by any of the wave function generators SCF, RASSCF, MRCI or CPF. You could also use MBPT2 or CASPT2. This approach has been used in the generation of the ANO-RCC basis sets. Your specific requirements dictate the choice of wave function generator, but MRCI would be most commonly used.
You are not restricted to atomic calculations but
can mix molecular and atomic calculations freely.
The restrictions are that the name of the center, for which
you are constructing a basis set, must be the same
in all wave functions.
The center may not be ``degenerate'', i.e.
it may not generate other centers through symmetry
operations. See the description of SEWARD
on page ![[*]](crossref.png) for a more extensive discussion.
For example for
for a more extensive discussion.
For example for 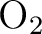 you cannot use D2h symmetry
since this would involve one center that is mirrored into the other.
Another restriction is, of course, that you must use the
same primitive set in all calculations.
you cannot use D2h symmetry
since this would involve one center that is mirrored into the other.
Another restriction is, of course, that you must use the
same primitive set in all calculations.
8.18.1 Dependencies
GENANO needs one or more wave functions in the form of natural orbitals. Thus you need to run one or more of SCF, RASSCF, MRCI or CPF. You could also use, for example, MBPT2 or CASPT2 but this is in general not recommended. GENANO also needs the one electron file ONEINT and the RUNFILE generated by SEWARD.
8.18.2 Files
Below is a list of the files that GENANO reads/writes. Files ONEnnn, RUNnnn and NATnnn must be supplied to the program. Files ANO and FIG are generated. File PROJ is an optional input file.
8.18.2.1 Input files
| File | Contents |
| RUNnnn | This file contains miscellaneous information for the nnn'th wave function, generated by the program SEWARD. One file per wave function must be supplied, RUN001, RUN002, .... |
| ONEnnn | This file contains the one-electron integrals corresponding to the nnn'th wave function, generated by the program SEWARD. One file per wave function must be supplied, ONE001, ONE002, .... |
| NATnnn | This file contains the natural orbitals corresponding to the nnn'th wave function, generated by the appropriate wave function generating program. One file per wave function must be supplied, NAT001, NAT002, ... |
| PROJ | This file contains orbitals used for projection of the densities. Needs to be available if the keyword PROJECT is specified. It is compatible in format with the file ANO, and can thus be the the file ANO from a previous run of GENANO. |
8.18.2.2 Output files
| File | Contents |
| FIG | This file contains a PostScript figure file of eigenvalues. |
| ANO | This file contains the contraction coefficient matrix organized such that each column correspond to one contracted basis function. |
8.18.3 Input
The input file must contain the line
&GENANO
right before the actual input starts. Below is a list of the available keywords.
Please note that you can not abbreviate any keyword.
| Keyword | Meaning |
| TITLE | This keyword starts the reading of title lines, with no limit on the number of title lines. Reading the input as title lines is stopped as soon an the input parser detects one of the other keywords. This keyword is optional. |
| SETS | This keyword indicates that the next line of input contains the number of sets to be used in the averaging procedure. This keyword must precede WEIGHTS if both are supplied. This keyword is optional, with one set as the default. |
| CENTER | This keyword is followed, on the next line, by the atom label for which the basis set is to be generated. The label must match the label you supplied to SEWARD. In previous versions of GENANO this label had to be in uppercase, but this restriction is now lifted and the case does not matter. This keyword is compulsory. |
| ROWWISE | This keyword makes GENANO produce the contraction coefficients row-wise instead of column-wise as is the default. This keyword is optional. |
| WEIGHTS | This keyword must be subsequent to keyword SETS if both are supplied. This keyword is optional, with equal weight on each of the sets as default. |
| PROJECT | This keyword states that you want to project out certain degrees of freedom from the density matrix. This can be useful for generating, for example, node less valence orbitals to be used with ECP's. If this keyword is specified, you must supply the file PROJ obtained as file ANO from a previous GENANO calculation, for instance. This keyword is optional. |
| LIFTDEGENERACY | This keyword will modify the occupation numbers read from
the orbitals files. The purpose is to lift th
degeneracy of core orbitals to avoid rotations.
The occupation numbers are changed according to
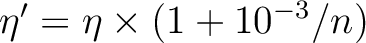 where n is the sequence number of the orbital
in its irreducible representation.
This keyword is optional.
where n is the sequence number of the orbital
in its irreducible representation.
This keyword is optional.
|
| RYDBERG | This keyword enables automatic generation of rydberg orbitals. With this keyword all occupied orbitals will get occupation number zero while the virtual orbitals will get a small occupation number decreasing with orbital number. Useful with a calculation on an cation where the virtual orbitals are near perfect rydberg orbitals. Note that you must use orbitals from the SCF or RASSCF program. This keyword is optional. |
| NOTHRESHOLD | This keyword is used to specify the threshold for keeping NO's (natural orbitals). Orbitals with occupation numbers less than the threshold are discarded. The threshold is read from the line following the keyword. Default value is 1.0d-8. |
Below is a simple input example, where we construct an ANO basis set for the carbon atom. Two wave functions are used, the SCF wave function and the SDCI wave function for the ground state of the atom.
&SEWARD
Title
Carbon atom
Symmetry
x y z
Expert
Basis set
C..... / inline
6.0 2
10 10
5240.6353 782.20479 178.35083 50.815942 16.823562 6.1757760 2.4180490
.51190000 .15659000 .05480600
1. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 1. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 1. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 1. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 1. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 1. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 1. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 1. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 1. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 1.
6 6
18.841800 4.1592400 1.2067100 .38554000 .12194000 .04267900
1. 0. 0. 0. 0. 0.
0. 1. 0. 0. 0. 0.
0. 0. 1. 0. 0. 0.
0. 0. 0. 1. 0. 0.
0. 0. 0. 0. 1. 0.
0. 0. 0. 0. 0. 1.
3 3
1.2838000 .34400000 .09220000
1. 0. 0.
0. 1. 0.
0. 0. 1.
C 0.000000 0.000000 0.000000
End of basis
&SCF
Occupied = 2 0 0 0 0 0 0 0
&RASSCF
Symmetry = 4
Spin = 3
nActEl = 2 0 0
Frozen = 0 0 0 0 0 0 0 0
Inactive = 2 0 0 0 0 0 0 0
Ras2 = 0 1 1 0 0 0 0 0
LevShft = 0.00
LumOrb
Thrs = 0.1d-8 0.1d-4 0.1d-4
&MOTRA
LumOrb
Frozen = 1 0 0 0 0 0 0 0
&GUGA
Electrons = 4
Spin = 3
Inactive = 1 0 0 0 0 0 0 0
Active = 0 1 1 0 0 0 0 0
CiAll = 4
&MRCI
SDCI
>>COPY $Project.RunFile RUN001
>>COPY $Project.RunFile RUN002
>>COPY $Project.OneInt ONE001
>>COPY $Project.OneInt ONE002
>>COPY $Project.RasOrb NAT001
>>COPY $Project.CiOrb NAT002
&GENANO
Title
Carbon atom
Project
sets
2
Center
C
Weights
0.5 0.5
>>RM ONE001
>>RM ONE002
>>RM NAT001
>>RM NAT002
Next: 8.19 geo Up: 8. Programs Previous: 8.17 gateway


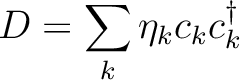
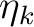 is the k'th eigenvalue (occupation value)
and ck is the k'th eigenvector (natural orbital).
The occupation number for a natural orbital is a
measure of how much this orbital contributes to
the total one-electron density.
A natural choice is to disregard the natural orbitals
with small occupation numbers and use those with large
occupation numbers to form contracted basis functions as
is the k'th eigenvalue (occupation value)
and ck is the k'th eigenvector (natural orbital).
The occupation number for a natural orbital is a
measure of how much this orbital contributes to
the total one-electron density.
A natural choice is to disregard the natural orbitals
with small occupation numbers and use those with large
occupation numbers to form contracted basis functions as