





















MOLCAS manual: Next: 8.39 qmstat Up: 8. Programs Previous: 8.37 numerical_gradient 8.38 poly_anisoThe POLY_ANISO program is a routine which allows a semi-ab initio description of the (low-lying) electronic structure and magnetic properties of polynuclear compounds. It is based on the localized nature of the magnetic orbitals (i.e. the d or f orbitals containing unpaired electrons [75,76]). For many compounds of interest, the localized character of magnetic orbitals leads to very weak character of the interactions between magnetic centers. Due to this weakness of the interaction, the metals' orbitals and corresponding localized ground and excited states may be optimized in the absence of the magnetic interaction at all. For this purpose, various fragmentation models may be applied. The most commonly used fragmentation model is exemplified in Scheme 1.
Magnetic interaction between metal sites is very important for accurate description of low-lying states and their properties. It can be considered as a sum of various interaction mechanisms: magnetic exchange, dipole-dipole interaction, antisymmetric exchange, etc. In the POLY_ANISO code we have implemented several mechanisms. The description of the magnetic exchange interaction is done within the Lines model [77]. This model is exact in three cases:
In addition to the magnetic exchange, magnetic dipole-dipole interaction can be accounted exactly, by
using the information about each metal site already computed ab initio. In the case of
strongly anisotropic lanthanide compounds, the dipole-dipole interaction is usualy the dominant
one. Dipolar magnetic coupling is one kind of long-range interaction between magnetic moments.
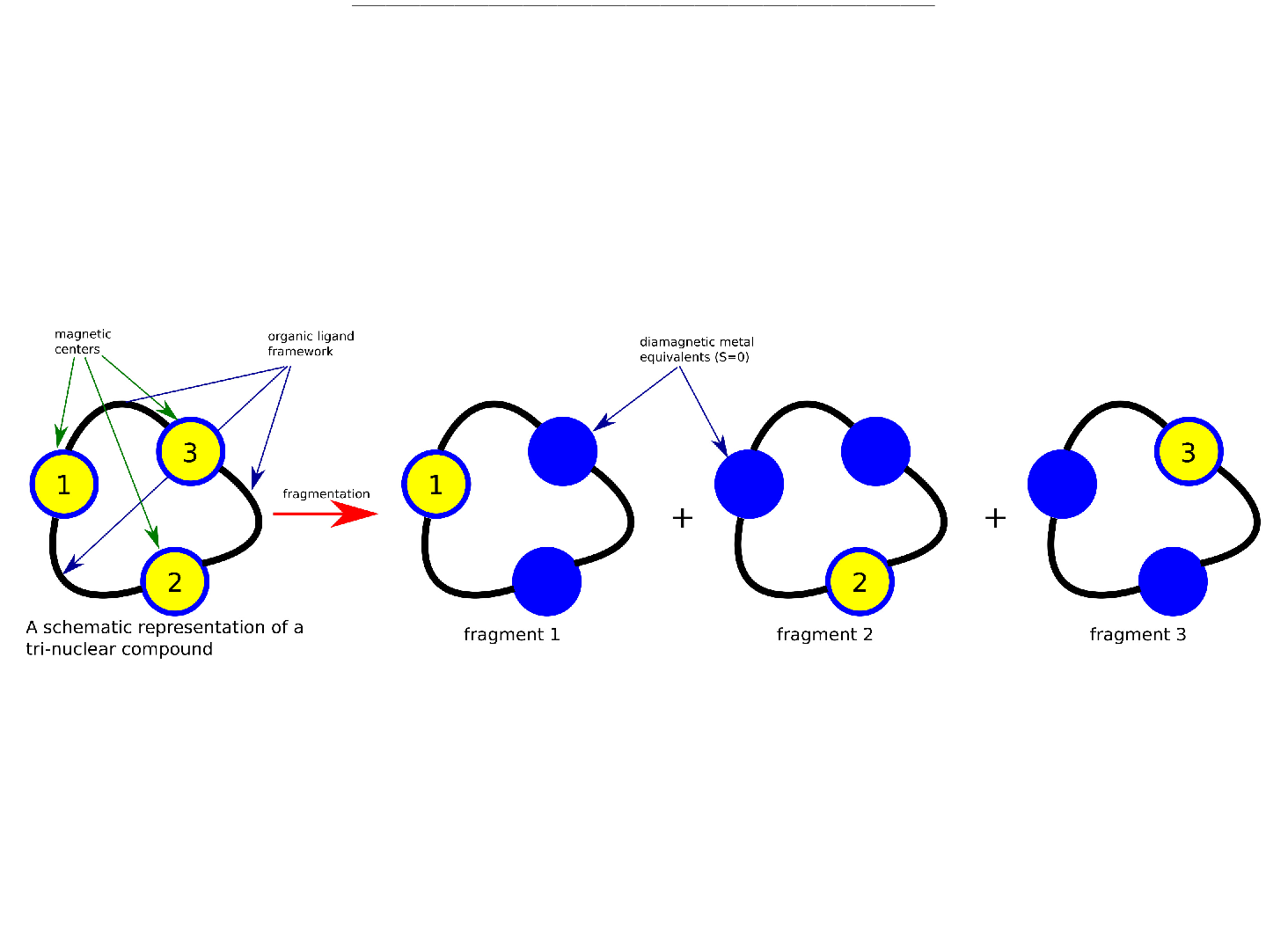
For example, a system containing two magnetic dipoles
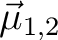 are the magnetic moments of sites 1 and 2, respectively; r is the distance between
the two magnetic dipoles, are the magnetic moments of sites 1 and 2, respectively; r is the distance between
the two magnetic dipoles, 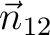 is the directional vector connecting the two magnetic dipoles (of unit length). is the directional vector connecting the two magnetic dipoles (of unit length).
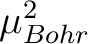 is the square of the Bohr magneton; with an approximative value of 0.43297 in cm-1/Tesla.
As inferred from the above Equation, the dipolar magnetic interaction depends on the distance and on the angle between the magnetic moments on magnetic
centers. Therefore, the cartesian coordinates of all non-equivalent magnetic centers must be provided in the input (see the keyword COOR). is the square of the Bohr magneton; with an approximative value of 0.43297 in cm-1/Tesla.
As inferred from the above Equation, the dipolar magnetic interaction depends on the distance and on the angle between the magnetic moments on magnetic
centers. Therefore, the cartesian coordinates of all non-equivalent magnetic centers must be provided in the input (see the keyword COOR).
8.38.0.1 Input filesThe program Poly_Aniso needs the following files:
8.38.0.2 Output files
This section describes the keywords used to control the standard input file.
Only two keywords NNEQ, PAIR (and SYMM if the polynuclear cluster has symmetry) are
mandatory for a minimal execution of the program, while the other keywords allow
customization of the execution of the POLY_ANISO.
|
| Keyword | Meaning | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| NNEQ | This keyword defines several important parameters of the calculation. On the first line after the keyword the program reads 2 values: 1) the number of types of different magnetic centers (NON-EQ) of the cluster and 2) a letter T or F in the second position of the same line. The number of NON-EQ is the total number of magnetic centers of the cluster which cannot be related by point group symmetry. In the second position the answer to the question: Have all NON-EQ centers been computed ab initio? is given: T for True and F for False. On the following line the program will read NON-EQ values specifying the number of equivalent centers of each type. On the following line the program will read NON-EQ integer numbers specifying the number of low-lying spin-orbit functions from each center forming the local exchange basis. Some examples valid for situations where all sites have been computed ab initio (case T, True):
Only in cases when some centers have NOT been computed ab initio (i.e. for which no aniso_i.input file exists), the program will read an additional line consisting of NON-EQ letters (A or B) specifying the type of each of the NON-EQ centers: A – the center is computed ab initio and B – the center is considered isotropic. On the following number-of-B-centers line(s) the isotropic g factors of the center(s) defined as B are read. The spin of the B center(s) is defined: S=(N-1)/2, where N is the corresponding number of states to be taken into the exchange coupling for this particular center. Some examples valid for mixed situations: the system consists of centers computed ab initio and isotropic centers (case F, False):
There is no maximal value for NNEQ, although the calculation becomes quite heavy in case the number of exchange functions is large.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| SYMM | Specifies rotation matrices to symmetry equivalent sites. This keyword is mandatory in the case more centers of a given type are present in the calculation.
This keyword is mandatory when the calculated polynuclear compound has exact crystallographic point group symmetry. In other words, when the number of
equivalent centers of any kind i is larger than 1, this keyword must be employed. Here the rotation matrices from the one
center to all the other of the same type are declared.
On the following line the program will read the number 1 followed on the next lines by as many 3x3 rotation matrices as the total number of
equivalent centers of type 1. Then the rotation matrices of centers of type 2, 3 and so on, follow in the same format.
When the rotation matrices contain irrational numbers (e.g. (
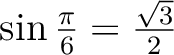 ), then more digits than presented in the examples
below are advised to be given: ), then more digits than presented in the examples
below are advised to be given:
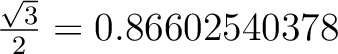 . .
Examples:
More examples are given in the Tutorial section.
|
Keywords defining the magnetic exchange interactions
This section defines the keywords used to set up the interacting pairs of magnetic centers and the corresponding exchange interactions.
A few words about the numbering of the magnetic centers of the cluster in the POLY_ANISO. First all equivalent centers of the type 1 are numbered, then all equivalent centers of the type 2, etc. These labels of the magnetic centers are used further for the declaration of the magnetic coupling. The pseudo-code is:
k=0
Do i=1, number-of-non-equivalent-sites
Do j=1, number-of-equivalent-sites-of-type(i)
k=k+1
site-number(i,j)=k
End Do
End Do
| Keyword | Meaning |
| PAIR or LIN1 |
Specifies the Lines interaction(s) between metal pairs. One parameter per interactiing pair is required.
|
| ALIN or LIN3 | Specifies the anisotropic interactions between metal pairs. Three parameters per interacting pair are required.
|
| LIN9 | Specifies the full anisotropic interaction matrices between metal pairs. Nine parameters per interacting pair is required.
|
| COOR | Specifies the symmetrized coordinates of the metal sites. This keyword enables computation of dipole-dipole
magnetic interaction between metal sites defined in the keywords PAIR, ALIN, LIN1, LIN3 or LIN9.
|
Other keywords
Normally POLY_ANISO runs without specifying any of the following keywords.
Argument(s) to a keyword are always supplied on the next line of the input file.
8.38.1.2 Optional general keywords to control the input
| Keyword | Meaning |
| MLTP | The number of molecular multiplets (i.e. groups of spin-orbital eigenstates) for which
g, D and higher magnetic tensors will be calculated (default MLTP=1).
The program reads two lines: the first is the number of multiplets (NMULT) and the
second the array of NMULT numbers specifying the dimension (multiplicity) of each multiplet.
Example:
|
| TINT |
Specifies the temperature points for the evaluation of the magnetic susceptibility. The program will read four numbers: Tmin, Tmax, nT, and
TINT 0.0 330.0 331 POLY_ANISO will compute temperature dependence of the magnetic susceptibility in 331 points evenly distributed in temperature interval: 0.0K – 330.0K.
|
| HINT | Specifies the field points for the evaluation of the magnetization in a certain direction. The program will read four numbers: Hmin, Hmax and nH
HINT 0.0 20.0 201 POLY_ANISO will compute the molar magnetization in 201 points evenly distributed in field interval: 0.0T – 20.0T.
|
| TMAG | Specifies the temperature(s) at which the field-dependent magnetization is calculated. Default is one temperature point, T=2.0 K.
Example:
TMAG 6 1.8 2.0 2.4 2.8 3.2 4.5
|
| ENCU | This flag is used to define the cut-off energy for the lowest states for which Zeeman interaction is taken into account exactly. The contribution to the magnetization coming from states that are higher in energy than E (see below) is done by second order perturbation theory. The program will read two integer numbers: NK and MG. Default values are: NK=100,MG=100.
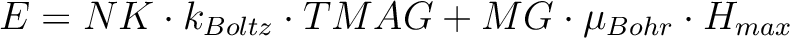
The field-dependent magnetization is calculated at the (highest) temperature value defined in either TMAG or HEXP. Example: ENCU 250 150 If Hmax = 10T and TMAG=1.8K, then the cut-off energy is: 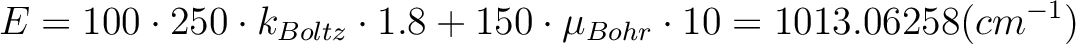
This means that the magnetization coming from all spin-orbit states with energy lower than E=1013.06258 (cm-1) will be computed exactly. ERAT, NCUT and ENCU are mutually exclusive.
|
| ERAT | This flag is used to define the cut-off energy for the lowest states for which Zeeman interaction
is taken into account exactly. The contribution to the molar magnetization coming from states that
are higher in energy than E (see below) is done by second order perturbation theory.
The program reads one real number in the domain (0.0-1.0). Default is 1.0 ( all exchange states are
included in the Zeeman interaction).
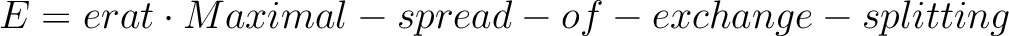
The field-dependent magnetization is calculated at all temperature points defined in either TMAG or HEXT. Example: ERAT 0.75 ERAT, NCUT and ENCU are mutually exclusive.
|
| NCUT | This flag is used to define the number of low-lying exchange states for which Zeeman interaction is taken into
account exactly. The contribution to the magnetization coming from the remaining exchange states is done by second
order perturbation theory. The program will read one integer number. The field-dependent magnetization is calculated at all temperature points defined in either TMAG or HEXT.
Example:
NCUT 125 In case the defined number is larger than the total number of exchange states in the calculation (Nexch), then nCut is set to be equal to Nexch. ERAT, NCUT and ENCU are mutually exclusive.
|
| MVEC | Defines the number of directions for which the magnetization vector will be computed.
On the first line below the keyword, the number of directions should be mentioned (NDIR. Default 0).
The program will read NDIR lines for cartesian coordinates specifying the direction i of the
applied magnetic field (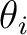 and and 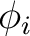 ). These values may be arbitrary real numbers.
The direction(s) of applied magnetic field are obtained by normalizing the length of each vector to one.
Example: ). These values may be arbitrary real numbers.
The direction(s) of applied magnetic field are obtained by normalizing the length of each vector to one.
Example:
MVEC 4 0.0000 0.0000 0.1000 1.5707 0.0000 2.5000 1.5707 1.5707 1.0000 0.4257 0.4187 0.0000 The above input requests computation of the magnetization vector in four directions of applied field. The actual directions on the unit sphere are: 4 0.00000 0.00000 1.00000 0.53199 0.00000 0.84675 0.53199 0.53199 0.33870 0.17475 0.17188 0.00000
|
| MAVE | This keyword specifies the grid density used for the computation of powder molar
magnetization. The program uses Lebedev-Laikov distribution of points on the unit sphere.[]
The program reads two integer numbers: nsym and ngrid. The nsym defines which
part of the sphere is used for averaging. It takes one of the three values: 1 (half-sphere),
2 (a quater of a sphere) or 3 (an octant of the sphere). ngrid takes values from 1
(the smallest grid) till 32 (the largest grid, i.e. the densiest). The default is to
consider integration over a half-sphere (since M(H)=-M(-H)): nsym=1 and ngrid=15
(i.e 185 points distributed over half-sphere). In case of symmetric compounds, powder
magnetization may be averaged over a smaller part of the sphere, reducing thus the number
of points for the integration. The user is responsible to choose the appropriate integration scheme.
Default value for grid-number=15 (185 directions equally distributed in the given area).
Note that the programś default is rather conservative.
|
| TEXP | This keyword allows computation of the magnetic susceptibility 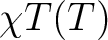 at experimental points.
On the line below the keyword, the number of experimental points NT is defined, and on the next NT lines the program reads the experimental temperature (in K) and the experimental magnetic susceptibility (in cm3Kmol-1 ). TEXP and TINT keywords are mutually exclusive. The magnetic susceptibility routine will also print the standard deviation from the experiment. at experimental points.
On the line below the keyword, the number of experimental points NT is defined, and on the next NT lines the program reads the experimental temperature (in K) and the experimental magnetic susceptibility (in cm3Kmol-1 ). TEXP and TINT keywords are mutually exclusive. The magnetic susceptibility routine will also print the standard deviation from the experiment.
TEXP READ number-of-T-points Do i=1, number-of-T-points READ ( susceptibility(i, Temp), TEMP = 1, number-of-T-points ) End Do
|
| HEXP | This keyword allows computation of the molar magnetization Mmol (H) at experimental points.
On the line below the keyword,the number of experimental points NH is defined, and on the next NH lines the program reads the experimental field intensity (Tesla) and the experimental magnetization (in 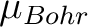 ). HEXP and HINT are mutually exclusive. The magnetization routine will print the standard deviation from the experiment. ). HEXP and HINT are mutually exclusive. The magnetization routine will print the standard deviation from the experiment.
HEXP READ number-of-T-points-for-M, all-T-points-for-M-in-K READ number-of-field-points Do i=1, number-of-field-points READ ( Magn(i, iT), iT=1, number-of-T-points-for-M ) End Do
|
| ZJPR | This keyword specifies the value (in cm-1) of a phenomenological parameter of a mean molecular field acting on the spin of the complex (the average intermolecular exchange constant). It is used in the calculation of all magnetic properties (not for spin Hamiltonians) (Default is 0.0)
|
| PRLV | This keyword controls the print level.
|
Next: 8.39 qmstat Up: 8. Programs Previous: 8.37 numerical_gradient


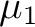 and
and 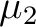 , separated by
distance
, separated by
distance 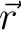 have a total energy:
have a total energy:
![\begin{displaymath}
E_{dip} = \frac{\mu_{Bohr}^{2}}{ r^{3}} [\vec\mu_{1} \cdot \...
... 3(\vec \mu_{1} \vec n_{12})\cdot (\vec \mu_{2} \vec n_{12})],
\end{displaymath}](img129.png)
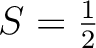 );
of the second center 2.43 (
);
of the second center 2.43 (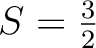 ); of the fifth center 2.00 (
); of the fifth center 2.00 ( , where
, where 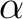 and
and 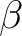 are main values of the Cartesian components of the (3x3) matrix defining the exchange interaction between site-1 and site-2.
are main values of the Cartesian components of the (3x3) matrix defining the exchange interaction between site-1 and site-2.
 .
.